Utilidad de los sistemas numericos

Introducción

Los números son como un lenguaje universal que utilizamos en nuestra vida diaria y en la tecnología que nos rodea. Sin embargo, existen diferentes formas de expresar y comprender esos números. En este artículo, exploraremos detalladamente cuatro sistemas numéricos distintos: el sistema decimal que usamos comúnmente, el sistema binario fundamental para las computadoras, el sistema octal con su singularidad y el sistema hexadecimal relacionado con colores y direcciones.

Sistema Decimal: La Base de la Cotidianidad

El sistema decimal, también conocido como base 10, es la forma de contar que utilizamos todos los días. ¿Recuerdas contar en tu infancia? 1, 2, 3, 4... eso es el sistema decimal en acción. Cada dígito representa un valor multiplicado por una potencia de 10. Por ejemplo, el número "315" en decimal se descompone en (3 * 10^2) + (1 * 10^1) + (5 * 10^0), que es igual a 300 + 10 + 5.

                    

Fuente: https://upload.wikimedia.org/wikipedia/commons/thumb/b/bc/Values_of_digits_in_the_Decimal_numeral_system.png/350px-Values_of_digits_in_the_Decimal_numeral_system.png

Sistema Binario: El Lenguaje de las Computadoras

El sistema binario, o base 2, es esencial para la electrónica y las computadoras. Aquí solo tenemos dos dígitos: 0 y 1. Esto puede parecer limitado, pero es perfecto para las computadoras, ya que utilizan señales de encendido (1) y apagado (0) para procesar información. Por ejemplo, el número "101" en binario se traduce a (1 * 2^2) + (0 * 2^1) + (1 * 2^0), que es igual a 4 + 0 + 1, lo que da como resultado 5 en decimal.

    

Fuente: https://www.tecnologia-informatica.com/wp-content/uploads/2018/02/sistema-binario.jpg

Sistema Octal: Un Enfoque Intermedio

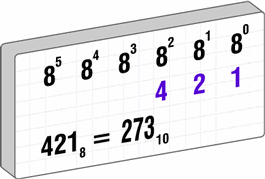
El sistema octal, o base 8, es menos común pero tiene sus aplicaciones. Imagina que estás contando en grupos de ocho. Los dígitos van del 0 al 7, y luego comienzan de nuevo. Este sistema es útil en la programación y en sistemas informáticos especiales. Por ejemplo, el número "27" en octal se traduce a (2 * 8^1) + (7 * 8^0), que es igual a 16 + 7, lo que da como resultado 23 en decimal.

Fuente: https://niixer.com/wp-content/uploads/2023/02/image-59.png

Sistema Hexadecimal: Colores y Más Allá

El sistema hexadecimal, base 16, es importante en campos como el diseño gráfico y la informática. Aquí, además de los dígitos del 0 al 9, usamos letras de la A a la F para representar valores mayores que 9. Cada dígito representa una potencia de 16. Por ejemplo, el número "1A" en hexadecimal se descompone en (1 * 16^1) + (10 * 16^0), que es igual a 16 + 10, resultando en 26 en decimal.

Fuente: https://eldiscretini.files.wordpress.com/2014/11/descarga.jpg?w=700

        

 Descubriendo la Variedad de la Numeración

Exploramos los sistemas numéricos desde diferentes ángulos. El sistema decimal es nuestro compañero diario, mientras que el sistema binario habla el lenguaje de las computadoras. El sistema octal ofrece una perspectiva intermedia, y el sistema hexadecimal desbloquea el mundo de los colores y las ubicaciones. Los números son como herramientas multifacéticas, utilizadas en diversas situaciones para comunicar información precisa y efectiva. 

Referencias

Video Sistemas Numericos explicacion y ejemplos 

Canal: Some School Games

Título del video: Sistemas Numericos explicacion y ejemplos 

Fecha de publicación: 12 de enero de 2013

URL del video: https://www.youtube.com/watch?v=nQh0BiZFcmM

Articulo sobre sistemas numericos 

Autor: José Luis Díaz González

Título de la página: Sistemas Numéricos

Fecha de publicación: No especificada

URL de la página: https://www.mat.uson.mx/~jldiaz/clip-1.2.SN.html